Accounting for Time
To best evaluate and justify long-term expenditures, HR should undersand how finance uses the keystone concept of net present value.
Time is money. We’ve all heard the saying, but in the world of finance it’s a governing principle.
A dollar today is worth more than a dollar tomorrow, because inflation erodes the buying power of money, and people would rather have things sooner than later. A dollar today is worth less than a dollar at some time in the past; we could have invested the dollar and received a return on it.
CFOs and other financial analysts use this principle to evaluate spending decisions, particularly capital investments. It’s at the heart of a key rule used to decide among competing uses of scarce funds: net present value (NPV).
NPV can involve elaborate equations and numerous projections and assumptions. It can appear daunting to those not trained in finance. Yet the concept behind the numbers and symbols is one that HR professionals should be familiar with as they attempt to work more closely with finance professionals and to create credible cost/benefit projections that help justify proposed HR programs and budgets (see "Business Partners").
Finance departments can help HR complete more complex NPV calculations, and gaining comfort with the concept will help HR partner better with CFOs and understand how they make decisions.
Use of NPV in calculations “gives you a systematic way to balance payments up front with gains later on,” says Robert A. Connolly, an associate professor of international finance and economics at the Kenan-Flagler Business School of the University of North Carolina at Chapel Hill. Finance departments—perhaps unbeknownst to HR—use NPV projections to compare “apples to oranges” in competing proposals from sales, marketing, production, IT and other departments, he says. The formulas translate dissimilar spending proposals into financial terms that are more comparable.
A Simple Example
The changing value of money over time is easily seen in the classic bank savings account.
If someone deposits $100 in a bank paying 10 percent interest per year, after one year the $100 starting amount increases $10 to a total of $110. If the money is left in the account for another year and the interest rate remains at 10 percent, the account increases by more because the entire $110 balance earns the 10 percent increase. The gain of $11 during the second year results in a new balance of $100nbsp; nbsp; + $10nbsp; nbsp; + $11, or $121.
To calculate how big the account would grow after several years, use the equation:
PV (1+r) t= FV
where PV is the present (or starting) value of the money, r is the interest rate, t is the time in years, and FV is the future value at the end of t years.
In the savings account example, if one wanted to determine how much money the $100 would grow to after four years at the interest rate of 10 percent, PV would be $100, 1+r would be 1 + 0.10, and t would be 4. The calculation of the future value:
$100 (1.10) 4 = $100 1.4641 = $146.41= $100 1.4641 = $146.41
Another way to look at this process is to ask how much money we would have to invest to come up with $146.41 after four years. The equation gets rearranged as:
PV = FV/(1+r) tor PV = $146.41/(1.10)4= $146.41/1.4641 = $100
Instead of compounding assets into the future, we are now “discounting” our end result back to the initial investment.
These examples of moving money around in time are at the heart of a basic rule of capital budgeting: Make investments that have a positive net present value, and don’t make investments that have a zero or negative NPV. Investments that produce positive NPV raise the firm’s net cash flow and increase stock prices and shareholder value.
Competing for Resources
But in the real world of business, investment decisions are far more complicated, and often more risky, than putting money in a savings account.
For example, if we want to invest $1 million this year in a project that will return several hundred thousand dollars each year for several years, does the project have a positive NPV? The answer depends on how much we get back and for how long, and calculations must take into account the varying cash flows in each of the years of the project as well as the expected cost of capital, which depends on the cost of debt and/or equity financing for the project. The cost of capital is usually provided by the CEO.
All of the future dollars to be earned must be converted in some way so that their values can be compared to the value of the current dollars that are to be spent, says Connolly. This is done on a spreadsheet that includes the interest or discount rate plus the expected cash flow for each year of the project. The cash flow is divided by the discount rate factor for each year, and the resulting numbers are added together. Subtracting the initial cost from that figure yields the NPV of the project. The equation for the calculation is:
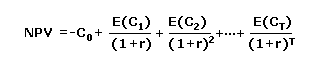
What if there are multiple investment opportunities? If there's enough investment capital, accept all that have positive NPVs. If there are competing proposals, evaluate them side by side to determine which have a positive NPV and which NPV is highest.
In the chart called "Evaluation of Three Strategies to Increase Retention", Connolly has calculated NPV for three different HR proposals to increase employee retention at a hypothetical company, using a variety of assumptions.
Option 1 would raise salaries by a substantial amount the first year and then by more modest amounts thereafter. The theory is that more highly compensated employees would be less likely to leave, less would be spent on replacement and training, and productivity would increase.
Option 2 would boost employee benefits, with only routine salary increases over the life of the program. Though the new costs would be lower than for raising salaries, the desired impact on employees from the benefits increase would be far less advantageous to the company under Connolly’s assumptions.
Option 3 would provide employees with training designed for their specific jobs. This alternative has the highest initial cash outlay, but its economic benefit far exceeds that of the first two options. The results are so dramatically different that even if some assumptions don’t pan out quite as expected, “there’s no discount rate that’s going to make this not work,” notes Connolly.
After using the NPV equation to compare the three options and finding that Option 1 has a small positive NPV, Option 2 has a negative NPV and Option 3 has a large positive NPV, Connolly did a fourth calculation for a combination of Options 1 and 3—raising salaries and providing special training.
The result is a positive NPV that is greater than if the NPVs of the two options were simply added together—a mathematical illustration of the value of synergy among programs that HR professionals often sense but cannot demonstrate definitively.
When all the alternatives are considered, “there’s no question which way to proceed,” says Connolly. “The assumption is that there’s an extra boost that you get when you pay people more and train people more. There’s an added incentive there,” and employees “get excited about the possibilities” of what they can accomplish with the double boost of compensation and training.
Connolly cautions that the results of this or any analysis are only as good as the assumptions behind the proposals. Changing the assumptions would mean changing some of the numbers, which could alter the recommendations. Thus, HR must be careful to make reasonable and defensible guesstimates of the costs and potential benefits of its proposals. Work with your finance department to test your assumptions and develop projections.
And remember that there is more to financial management than plugging numbers into NPV equations. Judging the risk of some proposed projects can be quite tricky, especially over longer time periods. The longer the time frame of a project, the greater the chances that future cash flows will differ from original estimates, particularly for the final years.
There are decisions to be made about how to raise the funds for the project. Planners must adjust the cost of capital for taxes and consider the potential for market forces, such as competitors’ actions, to alter expected project cash flows—a task that typically belongs to the CFO. And more.
But it all starts with net present value. Says Connolly: “It becomes a way systematically to organize your thinking” about where to invest precious resources.
Steve Bates is senior writer for HR Magazine.
Advertisement
An organization run by AI is not a futuristic concept. Such technology is already a part of many workplaces and will continue to shape the labor market and HR. Here's how employers and employees can successfully manage generative AI and other AI-powered systems.
Advertisement



